凌晨九点的世界
CSAPP深入理解计算机系统 Lab1(Data Lab) 详解
凌晨九点 Lv2
  2023-10-01 22:51:47   2024-04-12 23:33:45  

本文以记录个人学习CSAPP的过程，使用blog的方式记录能更专注的思考，不至于走马观花式的做实验。

实验说明

在动手实验之前建议仔细阅读实验提供的文档以及bits.c前的注释。本实验对应CSAPP的第二章，是对位运算的处理和应用。在解决这些问题过程中，会对位运算有更深刻的理解。实验中提供13个函数接口，我们需要根据函数前注释的要求实现相应的功能，同时满足所要求的限制条件。

环境配置

我的实验环境是Debian(x86_64)，编译32位的程序需要使用 sudo apt-get install gcc-multilib下载gcc-multilib，这是一个能够实现不同位数的编译器。下载后可以正常make编译。

实验中的工具dlc和driver.pl中可用-h参数查看使用手册

一些小坑

  1. 使用dlc时出现bits.c:xx:parse error bits.c:xx:undeclared variable xx 是因为该编译器仅仅支持C89的语法,需要将变量全部在代码块的开头声明。
  2. 使用dlc时出现bits.c:284: Warning: suggest parentheses around arithmetic in operand of x 是因为运算符优先级肯存在歧义，建议为优先运算块加括号

整数规则细节

表达式规则

  1. 整数的范围在0~255之间，不能使用大整数
  2. 只能使用局部变量和参数
  3. 允许使用单目运算符 ! ~
  4. 允许使用双目运算符 & ^ | + << >>

禁止使用

  1. 非顺序执行的语句
  2. 宏
  3. 调用函数
  4. 使用不在规定范围内的操作符
  5. 使用强制类型转换
  6. 使用非int类型，使用数组，结构体等

对运行机器的规定

  1. 使用补码，32位整数表示
  2. 按算术方式执行右移
  3. 如果移位数 大于31 或 小于0 , 移位有不可预测的行为

整数具体题解

1. bitXor

根据异或运算的表达式

A⊕B=(A∧¬B)∨(¬A∧B)A \oplus B = (A \land \lnot B) \lor (\lnot A \land B)

可知代码如下

1
2
3
4
5
6
7
8
9
10
11
12
/*
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4                                 
 *   Rating: 1   
 */
int bitXor(int x, int y) {
  int a = x & ~y;
  int b = ~x & y;
  int ans = ~(~a & ~b);
  return ans;
}

2. tmin

根据补码规则，最高位符号位为1时为负数，CSAPP上有一张图很好解释补码的规则image
所以根据这个规则我们知道最小的补数就是最高位为1，其余为0的数，实现代码如下

1
2
3
4
5
6
7
8
9
10
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
	int p = 1;
  return p << 31;
}

3. isTmax

  1. 同样根据上面的图可知，最大的数和最小的数在补数规则中是完全去反的规则，由此可以找出最大的数。要想不通过==比较两个数，我们可以采用异或后结果是否等于0的方式判断，因为只有相等才会异或为0。
  2. 但是本题禁止使用<<，代表我们需要采用另一种方式实现。我们令最大的数0x7fffffff为a。发现a+a = 0xffffffe(相当于右移一位)，对其去反的结果为1。顺着这个思路我们只需要找到其他满足~(x+x+1) == 0的数排除即可。不难思考，将0xffffffe右移的两种情况中的另一种为0xffffffff（也就是-1）,即-1 + 1 == 0，因此判断逻辑不难表达如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
 /* isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise 
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
  //判断想x+x+1取反后是否为0,tag可减少一个符号的使用
  int tag = x + 1;
  int tmp1 = ~(x + tag);
  int flag1 = !tmp1;
  //判断是否为-1
  int flag2 = !tag;
  //产生结果后
  return flag1 & !flag2;
}

4. allOddBits

题目需要找到所有奇数位都是1的数，可以通过移动一位后，判断或运算是否所有位都是1来判断结果,其中全位都是1就是-1，可以再简化判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* 
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  int t = 0xaa | (0xaa << 8) | (0xaa << 16) | (0xaa << 24);
  int a = x & t;
  int b = a >> 1;
  int c = a | b;
  int ans = !(c + 1);
  return ans;
}

5. negate

直接使用补码定义即可

1
2
3
4
5
6
7
8
9
10
/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) {
  return ~x + 1;
}

6. isAsciiDigit

主要思路是首先通过判断高位(4到7位)的为0011b,可以同时判断其他位是否为0,然后判断最后一位，观察发现（可以通过卡诺图辅助），满足条件的如下：满足0xxx (x表示任意)或者是8或9,实现代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/*
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
 *   Example: isAsciiDigit(0x35) = 1.
 *            isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x) {
  int y = x & 0xf;
  int z = (x >> 4);
  int flag1 = (!(y>>3)) | ( !(y ^ 8) | !(y ^ 9));
  int flag2 = !(z ^ 3);
  return flag1 & flag2 ;
}

上述的符号数为13，符合规定。但是观察发现，每次都需要使用!,我们可以通过摩根公式化简flag1,筛选掉不要的值，观察发现，在11xxb和1x1xb是需要剔除的元素,代码简化后如下,只需要11个符号

1
2
3
4
5
6
int isAsciiDigit(int x) {
  int flag1 = !((x & 0xa) ^ 0xa);
  int flag2 = !((x & 0xc) ^ 0xc);
  int flag3 = ((x >> 4) ^ 3);
  return !(flag1 | flag2 | flag3);
}

7. conditional

我们需要通过任何非1的数生成出0xffffffff(也就是-1)，同时0还是0。这个算法可以把思路转化为通过1生成0，通过0生成-1，那么也就-1对数减1即可。
具体可见代码注释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 
 * conditional - same as x ? y : z 
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
  //产生-1
  int neg = ~0;
  //!!x保证任何非0数为1，0还是0
  int mask = !!x + neg;
  //使用掩码的方式实现条件
  return (y & ~mask) | (z & mask);
}

8. isLessOrEqual

本题需要分为两种情况，两个数异号和同号，

异号的情况是如果相减会溢出，我们通过符号位的特点判断结果，观察发现，异号时结果和x的符号位同步

同号的情况相减判断符号位即可，这里的技巧是由于0和正数的符号位相同，因此采用y - x >= 0判断会简化过程

最后将两种情况通过掩码合并。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  //符号位
  int s1 = x >> 31;
  int s2 = y >> 31;
  //s1 == s2 ? 1 : 0
  int mask = !(s1 ^ s2);
  // y - x
  int diff = y + (~x) + 1;
  // y - x >= 0 ? 1 : 0
  int flag2 = !(diff >> 31);

  return (mask & flag2) | ((!mask) & (s1 & 1));
}

9. logicalNeg

本题需要充分利用符号位，由于最终需要实现的结果是逻辑非，如何识别出0就十分关键。在allOddBits一题最后我们通过为-1 + 1和0 + 1实现能让全1转换为0，全0转换为1的方法，本题同样借鉴这个思路。而0的特点是，其补码和就是其本身，具有同样特性的还有0x80000000(也就是前面找到的最小数），通过观察发现他们的区别在于最小数最小数和其补数做或运算后最高位为1，而0做相同运算后结果为0。再利用其符号右移的特性，能构造出需要的0xAAAAAAAA(全1)或0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* 
 * logicalNeg - implement the ! operator, using all of 
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int logicalNeg(int x) {
  int tag = x | (~x + 1);
  // 0xaaaaaaaa or 0
  int s = tag >> 31;
  // 0 or 1
  return s + 1;
}

10. howManyBits

首先我们可以通过给出的几组示例发现，对于任何数，相当于查看其原码表示的最小位数，我们可以先将负数转化为于之对应的补数，两者的最小表示位数相同，计算后记作y。

接着我们利用二进制数的表示思路来处理，也就是说，我们可以通过16、8、4、2、1这几个数表示1到31的任意数字，也就意味我们只要验证处理这几次就可以表示出位数来

处理时有技巧，我们从利用能取大的先取大的原则，不断缩小y(进行移位),如果不能移位则用小数再试。具体见代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
   int mask, y, tag16, tag8, tag4, tag2, tag1, has16bit, has8bit, has4bit, has2bit, has1bit;
  //mask = x < 0 ? 0xfffffffff : 0
  mask = (x >> 31);
  //为负数去反
  y = mask & (~x) | (~mask) & x;
  //判断是否满足16+1位 ? 1 : 0
  tag16 = !!(y >> 16);
  has16bit = tag16 << 4;
  y = y >> has16bit;
  //判断是否满足8位 ? 1 : 0
  tag8 = !!(y >> 8);
  has8bit = (tag8 << 3);
  y = y >> has8bit;
  //判断是否满足4位 ? 1 : 0
  tag4 = !!(y >> 4);
  has4bit = tag4 << 2;
  y = y >> has4bit;
  //判断是否满足2位 ? 1 : 0
  tag2 = !!(y >> 2);
  has2bit = tag2 << 1;
  y = y >> has2bit;
  //判断是否满足1位 ? 1 : 0
  tag1 = !!(y >> 1);
  has1bit = tag1 << 1;
  y = y >> has1bit;
  return has16bit + has8bit + has4bit + has2bit + has1bit + y + 1;
}

至此10道整数问题结束

浮点数规则细节

可以使用

  1. 可以使用循环和条件控制
  2. 使用int和unsigned，并可以使用任何运算符号

禁止使用

  1. 宏
  2. 定义或调用函数
  3. 使用非int和unsigned类型的数据
  4. 使用任何浮点运算符号

浮点数具体题解

1. floatScale2

只要熟悉浮点的规则就可以模拟出这个过程。

首先处理特殊情况（INF,NAN），其特点为M为0xff，此时返回这个数即可。

然后处理非标准数，需要确定是否会变成标准数，只要看E是否超过0x7fffff（也就是E所能表示的最大值即可）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/* 
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
  unsigned s, M, E, ans;
  //分解出s, M, E
  s = uf >> 31;
  M = (uf >> 23) & (0xff);
  E = uf & (0x7fffff);
  
  if(M == 0xff){ // NaN、Infinity的情况
    return uf;
  }else if(M == 0){ //非规格化的情况
    E = E << 1;
    if(E > 0x7fffff){ // 判断是否会变成规格化
      M = M + 1;
      E = E - 0x800000;
    }
  }else{ //规格化的情况
    M = M + 1;
  }
  ans = (s<<31) | (M << 23) | E;
  return ans;
}

floatFloat2Int

本题需要熟悉计算从浮点数转换为整数的规则，经过分析可以分为以下几种情况，

  1. 特殊值 NaN 和 infinity 的情况，会返回0x80000000u
  2. 非标准化的情况会返回0，因为非标准化表示的是小于1的数
  3. 实际阶数 a 满足a < 0的数同样返回0，因为表示的数同样小于1
  4. 实际阶数 a 满足0 <= a <= 23的情况，保留整数部分的数，具体计算规则见代码
  5. 实际阶数 a 满足a > 23，根据题目要求返回0x80000000u

其中非特殊情况还要加上符号位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/* 
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
  unsigned s, M, E ;
  int ans, a;
  //分解出s, M, E
  s = uf >> 31;
  M = (uf >> 23) & (0xff);
  E = uf & (0x7fffff);
  a = M - 127; //a表示实际的阶数

  if(M == 0xff){ // NaN、Infinity的情况
    return 0x80000000u;
  }else if(M == 0){ //非规格化的情况
    ans = 0;
  }else if(a < 0){ // 阶数为负的情况
    ans = 0;
  }else if (a <= 23){ //阶数符合整数规则的情况
    ans = (E >> (23 - a)) + (1 << a);
    // printf("0x%x %d %d\n",uf, ans, a+1);
  }else{ //阶数溢出的情况
    return 0x80000000u;
  }
  if(s){
     ans = -ans;
  }
  return ans;
}

3.floatPower2

一个小坑 :出现Timed out after 10 secs (probably infinite loop)的情况，应该是虚拟机性能不佳，绝对时间的超时。可以使用参数-T 20将执行限制时间改为20秒即可。

本题需要实现一个浮点数对2的幂计算，我们容易想到的是，浮点数本身计数方式就是以2的幂次形式，因此通过改变其中M的部分就可以实现大部分浮点运算。很容易想到的是当超出最大能表示数时返回0x7f800000（即无限大），当小到无法表示时，输出0。

但是事实上如果仅仅考虑阶数的问题，其实并没有得到正确答案，尽管这样做可以通过官方测试案例，但并不是正确答案。其实不应只靠考虑标准浮点数，非标准浮点数同样也应该考虑在内，我们把x + 121记作M，也就是真实阶数数，当阶数在0 =< M <= 23时能用非标准浮点数表示，详见代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/* 
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 * 
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while 
 *   Max ops: 30 
 *   Rating: 4
 */
unsigned floatPower2(int x) {
  unsigned  ans; 
  //真实的阶数
  int M = x + 127;
  if(M > 0xff){ //表示无穷大
    ans = 0x7f800000;
  }else if(M  > 0){ // 表示在标准浮点数表示的部分
    ans = M << 23;
  }else if(M > -23){ // 表示在非标准浮点数表示的部分
    ans = 1 << (M + 22);
  }else{ // 小于浮点数表示的部分
    ans = 0;
  }
  return ans;
}

为了验证函数的正确性，我写了一个验证程序mytest.c在项目目录下简单测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include "tests.c"
#include "bits.c"
#include <assert.h>
#include <stdio.h>
//每种情况的测试数据
int test_data[] = {0xfff, 12 - 127, 0 - 127, -20 - 127 , -23 - 127};

int main(){
  int size = sizeof(test_data) / sizeof(int);
  //重点测试数据
  for(int i = -50; i < 100; ++i){
    unsigned a, b;
    a = test_floatPower2(i-127);
    b = floatPower2(i - 127);
    printf("0x%u 0x%u\n", a, b);
    assert(a == b);
  }
  //自定数据测试
  for(int i = 0; i < size ; ++i){
    unsigned a, b;
    a = test_floatPower2(i);
    b = floatPower2(i);
    printf("0x%u 0x%u\n", a, b);
    assert(a == b);
  }
}

我们通过gcc -m32 -o mytest mytest.c编译后并执行./mytest。结果没有abort，一定程度验证正确性。

总结

最后附上最终测试结果
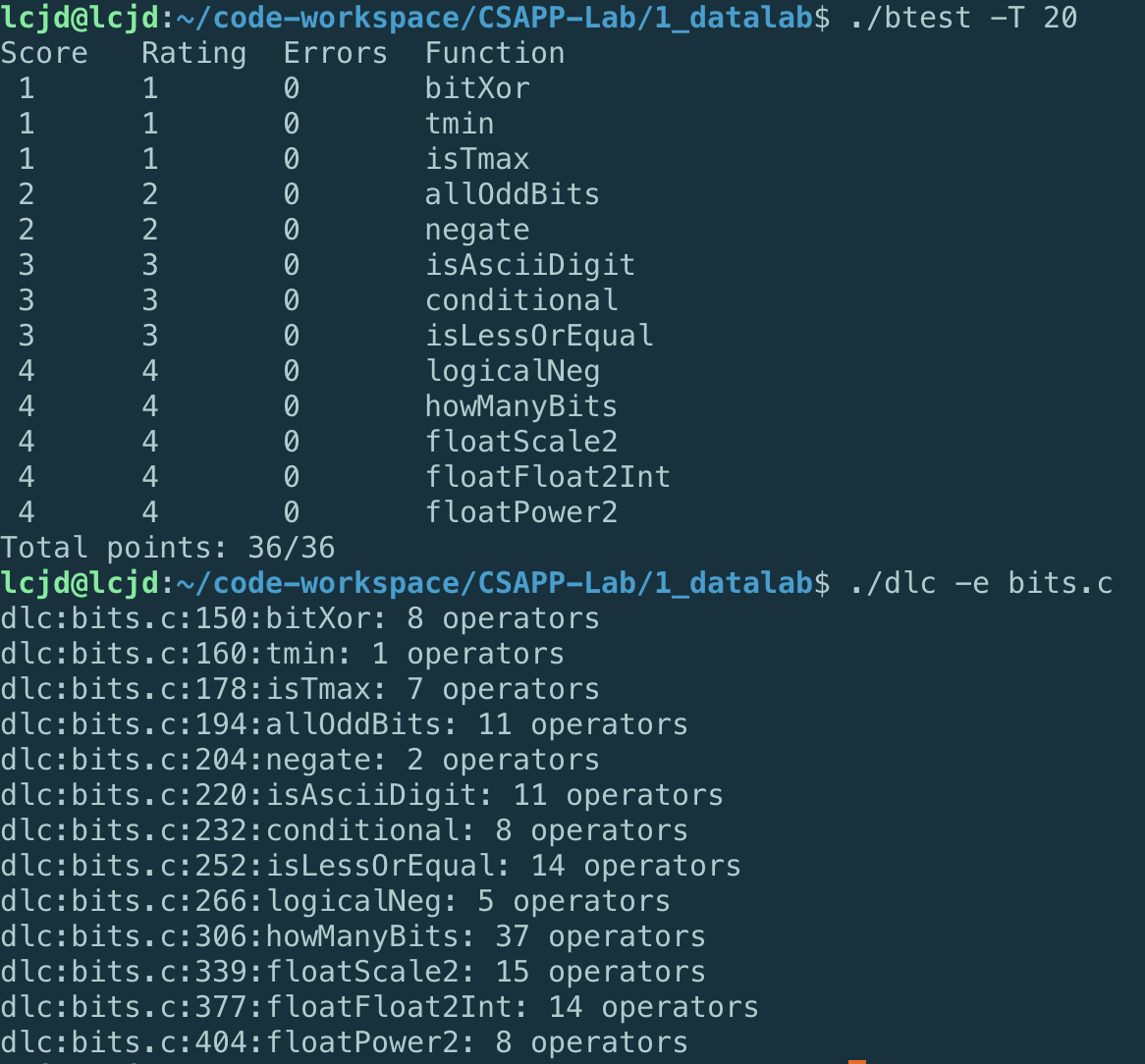
image

陆陆续续用了一周时间完成Lab1，我认为对计算机系统级的数据处理方式和技巧都有所学习，其中很多答案可能不是最优答案，欢迎大家留言讨论，共同学习。

  •  C
  1. 实验说明
  2. 环境配置
  3. 一些小坑
  4. 整数规则细节
    1. 表达式规则
    2. 禁止使用
    3. 对运行机器的规定
  5. 整数具体题解
    1. 1. bitXor
    2. 2. tmin
    3. 3. isTmax
    4. 4. allOddBits
    5. 5. negate
    6. 6. isAsciiDigit
    7. 7. conditional
    8. 8. isLessOrEqual
    9. 9. logicalNeg
    10. 10. howManyBits
  6. 浮点数规则细节
    1. 可以使用
    2. 禁止使用
  7. 浮点数具体题解
    1. 1. floatScale2
    2. floatFloat2Int
    3. 3.floatPower2
  8. 总结
  1. 实验说明
  2. 环境配置
  3. 一些小坑
  4. 整数规则细节
    1. 表达式规则
    2. 禁止使用
    3. 对运行机器的规定
  5. 整数具体题解
    1. 1. bitXor
    2. 2. tmin
    3. 3. isTmax
    4. 4. allOddBits
    5. 5. negate
    6. 6. isAsciiDigit
    7. 7. conditional
    8. 8. isLessOrEqual
    9. 9. logicalNeg
    10. 10. howManyBits
  6. 浮点数规则细节
    1. 可以使用
    2. 禁止使用
  7. 浮点数具体题解
    1. 1. floatScale2
    2. floatFloat2Int
    3. 3.floatPower2
  8. 总结